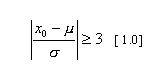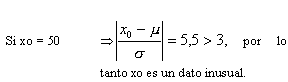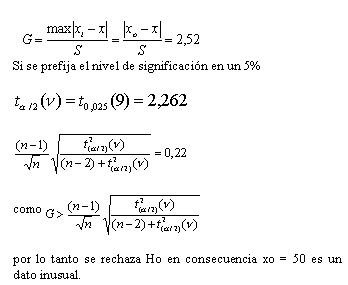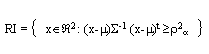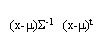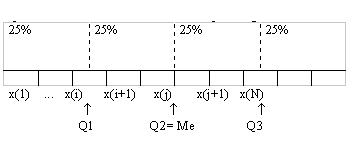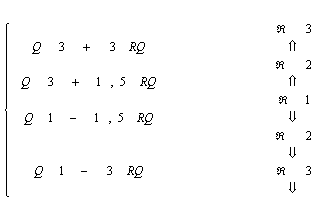La identificación de datos inusuales es un problema que recibe especial atención cuando se realizan estudios experimentales ya que la presencia de los mismos podría conducir a conclusiones erróneas.
Se analizaron y se aplicaron distintas técnicas estadísticas para la identificación y tratamiento de datos inusuales, además se tuvo en cuenta la sensibilidad de las mismas y los pasos a seguir para una correcta interpretación.
Procesamiento de datos estadísticos: "Búsqueda de datos inusuales".
Adriana Elias.
Cátedra de Biestadistica, Instituto de Matemática, Facultad de Bioquímica, Química y Farmacia, Universidad Nacional de Tucumán. Ayacucho 471, (4000) S. M. de Tucumán, Argentina.
PALABRAS CLAVE: Datos Inusuales, estadística Clásica, estadística Robusta
La identificación de datos inusuales es un problema que recibe especial atención cuando se realizan estudios experimentales ya que la presencia de los mismos podría conducir a conclusiones erróneas. Se analizaron y se aplicaron distintas técnicas estadísticas para la identificación y tratamiento de datos inusuales, además se tuvo en cuenta la sensibilidad de las mismas y los pasos a seguir para una correcta interpretación.
Introducción
En general en estudios observacionales se desea analizar el comportamiento de un lote de datos que surgen del estudio de una o más variables bajo ciertas condiciones; para ello podemos utilizar distintas técnicas estadísticas, entre ellas se encuentran las denominadas clásicas las que son muy sensibles frente a la presencia de datos inusuales. Esta situación nos conduce a las siguientes preguntas: ¿Qué es un dato inusual?, ¿Cómo se detecta?, ¿Una vez identificado debemos desecharlo?. Para poder tomar una decisión acertada es necesario recurrir a definiciones de ciertos conceptos y métodos estadísticos basados en el concepto matemático de distancias entre puntos, todo esto sin perder de vista que se debe implementar una acción adecuada acorde al proceso bajo estudio ya que la presencia de datos inusuales podría deberse al azar o a un comportamiento diferente que nos podría estar indicando alguna situación en particular. En consecuencia, podemos decir : es muy importante detectar la existencia o no de datos inusuales, como asimismo explicar su aparición, y la decisión que se tomara respecto a su tratamiento.
De esta manera, la identificación y tratamiento de un dato inusual puede ser considerada como un desafió, ya que la selección de la técnica a utilizar no es algo trivial, involucra un trabajo detectivesco que requiere paciencia y experiencia.
El objetivo de este trabajo es entonces : analizar distintos criterios basados en técnicas estadísticas que permitan la identificación de datos inusuales , como así también la sensibilidad y alcance de las mismas.
Datos Inusuales
Podemos definir informalmente como Inusual al dato que parece ser inconsistente con el resto del lote de datos bajo estudio, o como aquel dato que se encuentra muy disperso del conjunto de datos al que pertenece, lo que genera la sospecha que fue provocado por un mecanismo diferente que el resto de los datos. Puede presentarse en estudios univariados, bivariados o multivariados (Hawkins 1980).
Un dato inusual puede ser identificado a partir de tres categorías [Shashi Shekhar, et al, 2001]:
1) De un conjunto de datos univariados.
2) De un conjunto de datos multivariados basado en espacios multidimensionales.
3. - de gráficos multidimensionales ( en esta presentación consideraremos solo para datos bidimensionales ya que para otras dimensiones se debe tener en cuenta geometrías multidimensionales).
Las causas de la presencia de un dato inusual pueden ser consideradas en dos categorías (Hogjun Lu, et. al) :
1. - Contexto independiente : cuando no se observa comportamientos sistemáticos en los datos inusuales, por lo que es posible pensar que su presencia es debido al azar, usualmente causados por errores inesperados, por errores humanos o de los instrumentos de medición. En estos casos se debe repetir el estudio, si la discrepancia desaparece el error se debe a errores posiblemente humanos o del instrumental usado, pero si la discrepancia se mantiene debemos preguntarnos los motivos de la presencia del mismo, en este caso se puede separar dicho dato del resto y ser analizado para luego ser desechado o no según el criterio del investigador.
2. - Contexto dependiente : cuando se observan disparidades sistemáticas , las cuales podrían surgir como consecuencia de la presunción de conflictos o de la presencia de un sistema diferente, en este caso los datos inusuales se deben separar y considerar que estamos en presencia de un sistema o teoría diferente, se deben analizar como un conjunto distinto para ser estudiado y comparado con el resto de los datos.
Para tratar de determinar las causas de la presencia de un dato inusual debemos realizarnos las siguientes preguntas:
*¿Hemos cometido algún error al registrar dicho dato?
*¿Se presento algún problema al realizar el experimento?
*¿Dicho dato se presento debido a la diversidad biológica?
*¿Porqué es diferente?
*¿Qué significa ser diferente?
*¿El o los datos inusuales presentes proveen información respecto a la materia bajo estudio?.
*¿El o los datos inusuales presente estarán indicando algún aspecto previo que no consideramos?.
Métodos estadísticos
Existen algunos métodos estadísticos para detectar datos inusuales, “todos estos métodos se basan en cuan lejos se encuentran del resto de los datos o de algún dato en particular”. Podemos definir como regla de identificación de un dato inusual (Knorr, Ng. , 1997):
Dado un conjunto de datos T, sea O un dato del conjunto T, diremos que es inusual si al menos una fracción p de datos que en T están por lo menos a una distancia D de O.
Esta definición es intuitiva porque captura el espíritu general de un dato inusual, es decir que considera cualquier dimensión de la cual provengan los datos, como así también la función de distancia.
Datos Univariados
Sea x(1), x(2), . . . , x(n) un lote de n datos ordenados en forma creciente que provienen de una Población con distribución :
I) Desconocida
II) Conocida
I) Población con Distribución desconocida
En este caso se utilizan las técnicas del análisis exploratorio de datos. Podemos decir que el análisis exploratorio pretende encontrar pistas, sugerencias, ideas e hipótesis que tengan una significación teórica, sobre la realidad que describen numéricamente las distribuciones del lote de datos bajo estudio.
En el análisis exploratorio para detectar un dato de comportamiento inusual y clasificarlo como “alejado” o “muy alejado”, se deben calcular los Cuantiles denominados Cuartiles, estos se consideran como las medidas de posición que dividen al lote de datos en cuatro partes iguales.
Q1 ( Primer Cuartil, deja a su izquierda un 25% del lote de datos y a su derecha un 75%).
Q3 (Tercer Cuartil, deja a su izquierda un 75 % del lote de datos y a su derecha un 25%).
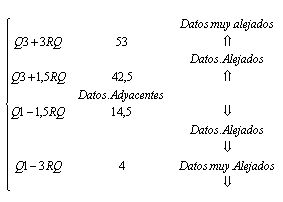
Una vez conocidos Q1 y Q3 es posible definir cada una de las tres regiones denominadas: a) Â1º Región de datos adyacentes, b)Â2º Región de datos Alejados y c)Â3º Región de datos muy alejados. Estas regiones se basan en las distancias de 1, 5 y 3 veces el rango intercuartil respecto al primer y tercer cuartil.
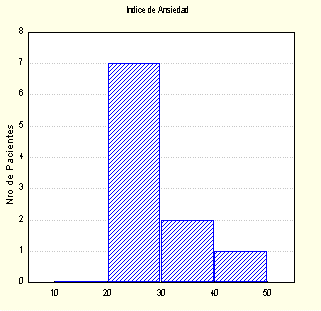
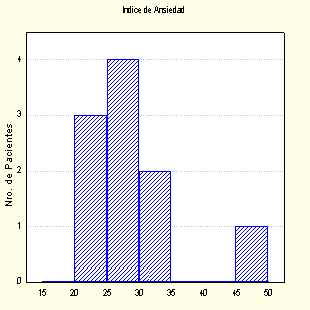
Ejemplo: Sean los siguientes valores de un índice de ansiedad correspondiente a un grupo de pacientes de sexo femenino que presentan el primer estadio de la enfermedad de Alzheimer: 25, 28, 28, 22, 29, 26, 25, 32, 35, 31, 50
Nota: altos valores del índice indican altos valores de ansiedad.
Si representamos gráficamente los datos en Histogramas con 5 y 8 clases, obtendremos:
Gráf. 1 ( 5 clases)
Graf. 2 (8 clases)
Es posible notar que en el gráfico Nro. 2 se presenta una clase separada del resto, esto nos podría estar indicando la presencia de un dato inusual lo que no se observa en el 1er gráfico, por lo que es posible concluir que un histograma es un gráfico muy sensible al número de clases seleccionado en consecuencia debemos recurrir a otro tipo de representación gráfica.
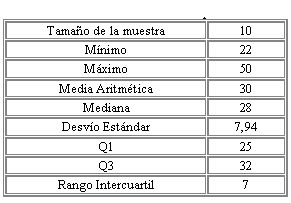
El análisis exploratorio da énfasis al estudio de un lote de datos utilizando técnicas gráficas en particular las denominadas “Diagramas de Tallo y Hojas”, “Box - Plot” ambas técnicas tienen en cuenta las regiones de Datos Adyacentes, Alejados y Muy Alejados, definidas anteriormente. A partir de la siguiente tabla de medidas descriptivas es posible encontrar a Â1 , Â2 , y Â3
Tabla No 1: Medidas descriptivas
al analizar los datos sin agrupar es posible detectar que el índice de ansiedad igual a 50 es un dato alejado.
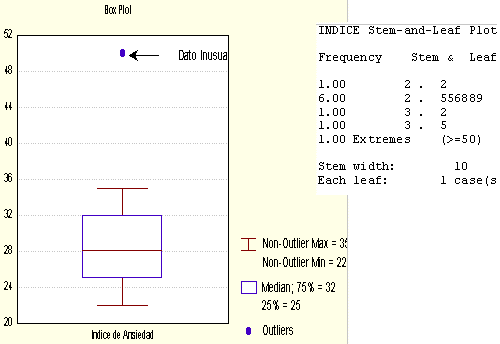
Utilizando cualquier programa estadístico standart es posible obtener:
En ambos gráficos se detecta al dato del Indice de ansiedad igual a 50 como un dato inusual.
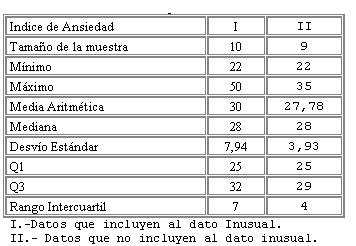
Con la finalidad de analizar la sensibilidad de las distintas medidas descriptivas es posible considerar la sig. tabla
Tabla Nro. 2: Medidas Descriptivas
Se puede observar que al separar el dato inusual es posible comparar como variaron algunas medidas de posición y de variabilidad obteniendo: a) Al comparar los desvíos podemos observar que la variabilidad ha disminuido en un 50, 5%.
b) La media aritmética disminuyo casi un 8% , sin embargo la mediana no sufrió cambios por lo tanto es posible concluir que la mediana es una medida de posición Robusta, es decir sufre pocos cambios frente a valores inusuales.
II) Población con Distribución Conocida
a)Definición: Sea x(1), x(2), x(3), . . . , x(n) un lote de n datos proveniente de población con distribución Normal con m media y s2 varianza conocidas, diremos que x0 perteneciente al lote de datos es un dato inusual si y solo si:
En esta definición es posible notar que una vez identificado x0 como un dato con un comportamiento diferente, al calcular [1. 0] estaremos estandarizando pero al mismo tiempo considerando la distancia Euclidiana de dos puntos en Â1.
En el ejemplo: Considere que los datos provienen de una población con distribución normal con m = 28 , s = 4
b) Sea x(1), x(2), x(3), . . . , x(n) un lote de n datos proveniente de población con distribución Normal con m media y s2 varianza desconocidas, diremos que x0 perteneciente al lote de datos es un dato inusual si se identifica y se comprueba con la prueba de Grubbs:
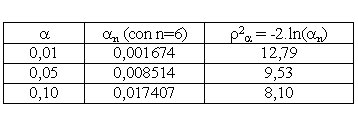
PRUEBA DE GRUBBS ( Método conocido como “Prueba de la desviación extrema estudentizada” en ingles ESD)
En el ejemplo
Datos Bivariados o Multivariados
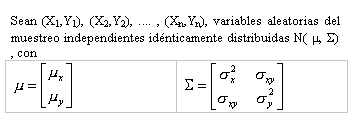
Para la identificación de datos inusuales en casos bivariados o multivariados , las expresiones algebraicas de distancias entre puntos se complican al aumentar la dimensión del espacio que generan las variables bajo estudio. Es así entonces, que en un gran número de trabajos se analizan distintas expresiones alcanzando la conclusión de que la distancia euclidiana produce buenos resultados para dimensiones pequeñas, como máximo hasta dos, en cambio si se aplica la distancia de Mahalanobis los resultados son mas confiables. En el presente trabajo a partir de una definición general dada por Davies y Gather en 1993, se particulariza para el caso bivariado con la finalidad de lograr una simplificación para una adecuada comprensión de la metodología a utilizar, es así que para analizar el procedimiento formal utilizaremos dos ejemplos que nos permitirán a partir de datos que surgen de distribuciones conocidas, que fueron contaminados con datos inusuales, la identificación de los mismos.
Región Inusual (Balakrishnan, Quiroz, 1997)
Note que para la aplicación de las definiciones anteriores el lector afrontara grandes dificultades si no cuenta con una formación matemática adecuada. Con la finalidad de realizar una simplificación analizaremos el caso Bivariado.
En general desconocidos, por lo que deben ser estimados.
Los estimadores que se sugieren son los que surgen de los datos recortados, es decir considerando el 90% de datos comprendidos entre el 5to y 95avo Percentiles, ya que los mismos son considerados robustos.
A partir de considerar Wn(0) es posible definir a la región de datos inusuales como
La expresión
se denomina distancia de Mahalanobis, a partir de ella se obtendrán n distancias, cada una correspondiente a cada dato observado, un dato será considerado como dato inusual si se encuentra en la región inusual. Además se cumple la propiedad
Ejemplos: A continuación consideraremos dos ejemplos en los cuales se observan las siguientes situaciones:
a)Un dato inusual fácilmente identificable, el cual debe ser separado del resto de los datos para no afectar en la estimación del modelo propuesto.
b)Dos datos inusuales no fácilmente identificables, los cuales podrían brindar información falsa respecto al modelo seleccionado, ya que si no se separan el mejor modelo a estimar seria exponencial, en cambio si se separan el mejor modelo a estimar sería lineal, por lo que resultaría muy riesgoso su no identificación. Considere los siguiente datos:
Ejemplo 1: (1, 2. 44); (2, 2. 98); (3, 3. 64); (4, 7. 45); (5, 5. 44); (6, 6. 64).
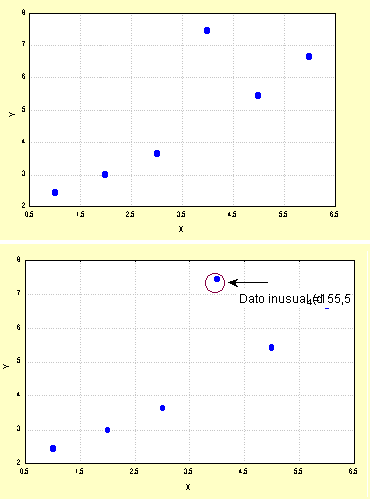
Ejemplo 2: (1, 2. 2); (2, 2. 4); (3, 2. 6); (4, 2. 8); (5, 5. 44); (6, 6. 64)
Si aplicamos la metodología propuesta para el cálculo de las distancias y consideramos:
Gráficamente obtendremos:
Ejemplo 1
Ejemplo 2
Por lo tanto es posible notar fácilmente que la técnica propuesta, identifica satisfactoriamente los datos inusuales simulados.
Nuevamente es necesario resaltar que si consideramos más de dos variables o si nos encontramos con un número importante de datos, debemos recurrir al apoyo de un programa de computación estadístico - Matemático , para poder aplicar las técnicas propuestas.
Conclusión
Se demostró aquí que la no detección adecuada de datos inusuales podrían conducirnos a interpretaciones erróneas sobre el grupo de datos bajo estudio, como así también que las técnicas estadísticas clásicas son muy sensibles a la presencia de datos alejados o muy alejados. En áreas de las Ciencias de la Salud es recomendable investigar muy cuidadosamente los motivos de la presencia de datos inusuales ya que los mismos podrían estar indicando que estamos frente a una teoría o hipótesis diferente.
Bibliografía
* Knorr Edwing M. , Ng Raymond T. , (1997), “ A Unified Notion of Outliers: Properties and Computation”, American Association for Artificial Intelligence, URL: www. aaai. org.
* Shashi Shekhar, Chang Tien Lu, Pusheng Zhang, (2001), “Detenting Graph-Based Spatial Outliers: Algorithms and Aplications (A summary of Results), URL: www. cs. umn. edu/pusheng/pub/kdd2001
* Cuadras C. M. , Arenas C. , (1990), “ A Distance Based regresión Model for Prediction with Mixed Data”, Comunications in Statistics A. Theory and Methods, 19, pp. 2261-2279.
* Becker C. , Gather U. , (1998), “The Larget Nonidentifiable Outlier: A Comparison of Multivariate Simultaneous Outlier Identification Rule”, URL:citeseer. nj. nec. com/301423. html
* Balakrishnan N. , Quiroz A. J. , (1997 ), “A procedur for outlier identifiction in data sets from continuous distributions”, URL:citeseer. nj. nec. com/301423. html
* Shashi Shekhar, Chang Tien Lu, Pusheng Zhang, (2001), “Detenting Graph-Based Spatial Outliers: Algorithms and Aplications”, URL: www. cs. umn. edu/Research/shashi-group
* Taplin Ross H. , (1998 ), “Model Selection for Time Series in the Presence of Outliers”, URL:citeseer. nj. nec. com/25360. html
* Rousseeuw P. , Hubert M. , (1997), “Recent developments in PROGRESS”, URL: win-www. uia. ac. be/u/statis
* Pena D. , Yohai V. , (1999), “A Fast Procedure for Outlier Diagnostics in Large regresión Problems”, Journal of the American Statistical Association. URL: www. amstat. org/publications/java/toc_99. htm
* Ballester P. , (1995), “Robust Data Analysis Methods for Spectroscopy”, Astronomical Data Analysis Software and Systems IV. Electronic Editor H. E. Payne.
* Graph Pad, “Grubbs Test for Detecting Outliers”. URL:www. graphpad. com/calculatos/GrubbsHowTo. cfm
*Annis C. , (2001 ), “Outliers”, URL:www. sttisticalengineering. com/outliers. htm
*Glossary of Terms, (1997), NWP Associates, Inc. URL:www. statlets. com/usermanual/glossary. htm
* Becker C. , Gather U. , (1997 ), “The Maximum Asymptotic Bias of Outlier Identifiers”, URL:citeseer. nj. nec. com/becker97maximun. html
*Knorr Edwing M. , Ng Raymond T. , Tucakov Vladimir, (1998 ), “ Distance based outliers: algorithms and applications, Point Grey Research Inc. , Canada. URL:citeseer. nj. nec. com/294396. html
IMPORTANTE: Algunos textos de esta ficha pueden haber sido generados partir de PDf original, puede sufrir variaciones de maquetación/interlineado, y omitir imágenes/tablas.